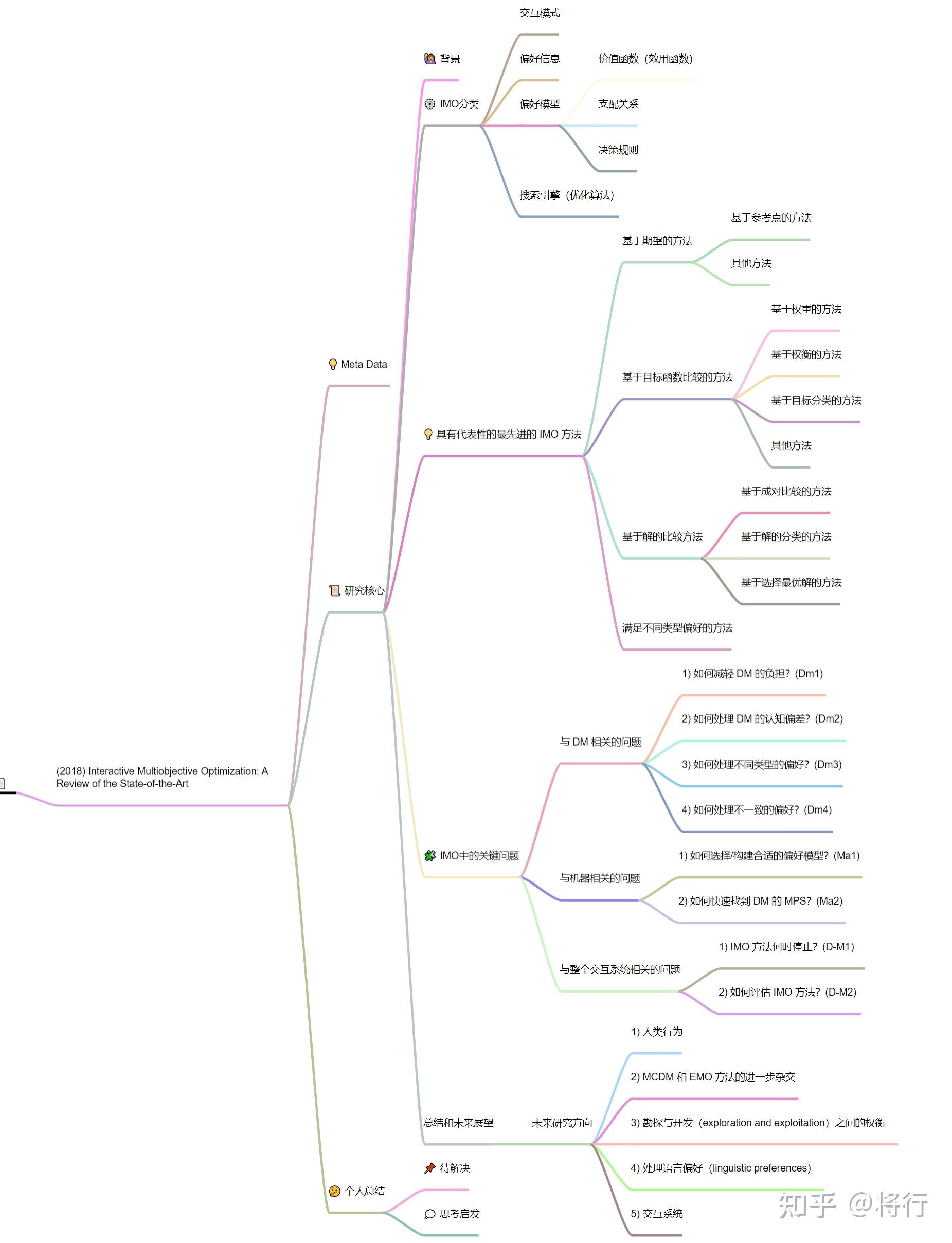
【精读笔记&翻译】交互式多目标优化: 最新技术综述
本文为笔者了解"人和算法交互”领域时接触的一篇综述文章:《Interactive Multiobjective Optimization: A Review of the State-of-the-Art》,为BIN XIN等人于2018年撰写的。该文结构清晰、直观易懂,令我受益匪浅,故记录。
本文仅为学习记录,若有不当之处请指出,在此也十分感谢原论文作者。
| 作者: Bin Xin; Lu Chen; Jie Chen; Hisao Ishibuchi; Kaoru Hirota; Bo Liu |
| 期刊: IEEE Access (发表日期: 2018) |
| 本地链接: Xin 等 - 2018 - Interactive Multiobjective Optimization A Review .pdf |
| DOI: 10.1109/ACCESS.2018.2856832 |
| 摘要: Interactive multiobjective optimization (IMO) aims at ?nding the most preferred solution of a decision maker with the guidance of his/her preferences which are provided progressively. During the process, the decision maker can adjust his/her preferences and explore only interested regions of the search space. In recent decades, IMO has gradually become a common interest of two distinct communities, namely, the multiple criteria decision making (MCDM) and the evolutionary multiobjective optimization (EMO). The IMO methods developed by the MCDM community usually use the mathematical programming methodology to search for a single preferred Pareto optimal solution, while those which are rooted in EMO often employ evolutionary algorithms to generate a representative set of solutions in the decision maker’s preferred region. This paper aims to give a review of IMO research from both MCDM and EMO perspectives. Taking into account four classification criteria including the interaction pattern, preference information, preference model, and search engine (i.e., optimization algorithm), a taxonomy is established to identify important IMO factors and differentiate various IMO methods. According to the taxonomy, state-of-the-art IMO methods are categorized and reviewed and the design ideas behind them are summarized. A collection of important issues, e.g., the burdens, cognitive biases and preference inconsistency of decision makers, and the performance measures and metrics for evaluating IMO methods, are highlighted and discussed. Several promising directions worthy of future research are also presented. |
| 笔记日期: 2024/1/14 下午8:32:35 |
摘要翻译
交互式多目标优化(IMO)旨在根据决策者逐步提供的偏好,找到其最喜欢的解决方案。在这一过程中,决策者可以调整自己的偏好,只探索搜索空间中感兴趣的区域。近几十年来,IMO 逐渐成为两个不同领域的共同关注点,即多准则决策(MCDM)和进化多目标优化(EMO)。多准则决策制定(MCDM)界开发的 IMO 方法通常使用数学规划方法来寻找单一的帕累托最优解,而那些植根于 EMO 的 IMO 方法通常使用进化算法来生成决策者偏好区域内一组有代表性的解。
本文旨在从 MCDM 和 EMO 两个角度对 IMO 研究进行综述。考虑到交互模式、偏好信息、偏好模型和搜索引擎(即优化算法)等四个分类标准,本文建立了一个分类标准,以确定重要的 IMO 因素并区分各种 IMO 方法。根据该分类法,对最先进的 IMO 方法进行了分类和回顾,并总结了这些方法背后的设计思想。重点讨论了一系列重要问题,如决策者的负担、认知偏差和偏好不一致,以及评估 IMO 方法的性能措施和指标。还介绍了值得未来研究的几个有前途的方向。
多目标优化的最终目标是支持决策者(DM)找到他或她最偏好的解决方案(MPS)。MPS指的是决策者优先于所有其他帕累托最优解的帕累托最优解。根据DM参与解决方案过程的阶段,多目标优化方法可以分为以下三类:先验方法、后验方法和交互式方法。其中,交互式方法是指DM逐渐在解决方案过程中指定偏好,以指导搜索朝着他/她偏好的区域发展。该方法克服了先验和后验方法的弱点,减少了计算复杂性和DM同时比较众多非支配解的负担。
MCDM社区开发的经典的 IMO 方法,如步骤法(STEM)[10]、Geoffrion-Dyer-Feinberg 法(GDF)[11]、交互式代用值权衡法(ISWT)[12]、参考点法[13]、满意权衡法(STOM)[14]、GUESS 法[15]、Zionts-Wallenius(Z-W)法和 NIMBUS 法[16]、[17]。关于这些方法的更多细节,读者可参阅[17]、[31]。一般来说,这些方法通过使用 DM 的局部偏好信息,在每次迭代时将 MOP 转化为单目标优化问题(SOP)。
MCDM和EMO两种方法的混合方式:“EA in MCDM”和“MCDM in EMO”。其中,“EA in MCDM”是指通过进化算法(EAs)来解决MCDM方法中的多目标优化问题,尤其是复杂问题(如非凸、不连续或非可微问题)。而“MCDM in EMO”则是借鉴MCDM方法的思想,将决策者的偏好信息先验地或交互式地导入多目标进化算法(MOEAs),以引导MOEAs找到逼近决策者偏好的帕累托前沿的解。
现有的 IMO 综述可能集中于 IMO 以外的更大领域,或者主要集中于 IMO 方法的一部分,即交互式 MCDM 方法和交互式 MOEAs。本文旨在从 "MCDM + EMO "的角度对 IMO 进行跨学科综述,根据系统分类法对这两个领域开发的 IMO 方法进行区分。
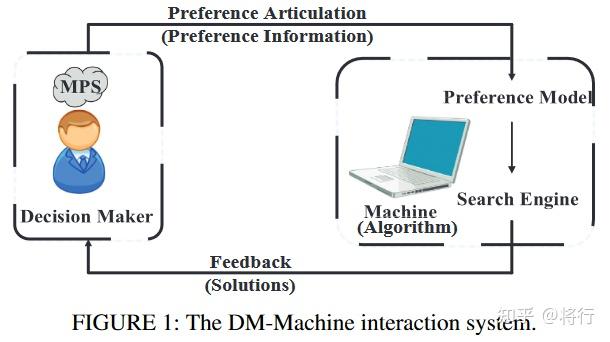
DM 指的是希望找到自己的 MPS 的人类 DM,而机器实际上是一种算法,包括偏好模型和搜索引擎(优化算法)。对 IMO 方法的以下四个基本设计因素进行系统分类:1) 交互模式;2) 偏好信息;3) 偏好模型;4) 搜索引擎
两种交互模式:搜索引擎完整运行后的交互(IAR)和运行过程中的交互(IDR)。在 IAR 中,DM 与机器的交互是由机器(算法)触发的,而在 IDR 中则更多地由 DM 控制
- IAR:两个相邻的相互作用之间执行一次完整的搜索引擎运行。如果只生成并向 DM 展示一个解决方案,DM 可以提供参考点、权重、权衡和目标分类等偏好。如果向 DM 展示了多个解决方案,他/她可以指定参考点或权重,就最喜欢的解决方案提供权衡或目标分类,并对这些解决方案进行比较,等等。
- IDR:DM 在搜索引擎运行期间定期提供偏好,以引导搜索朝向 DM 感兴趣的区域 (ROI)
目标的权衡和分类等偏好更适合于采用 IAR 模式的方法,因为在帕累托最优解中考虑目标之间的权衡更有意义
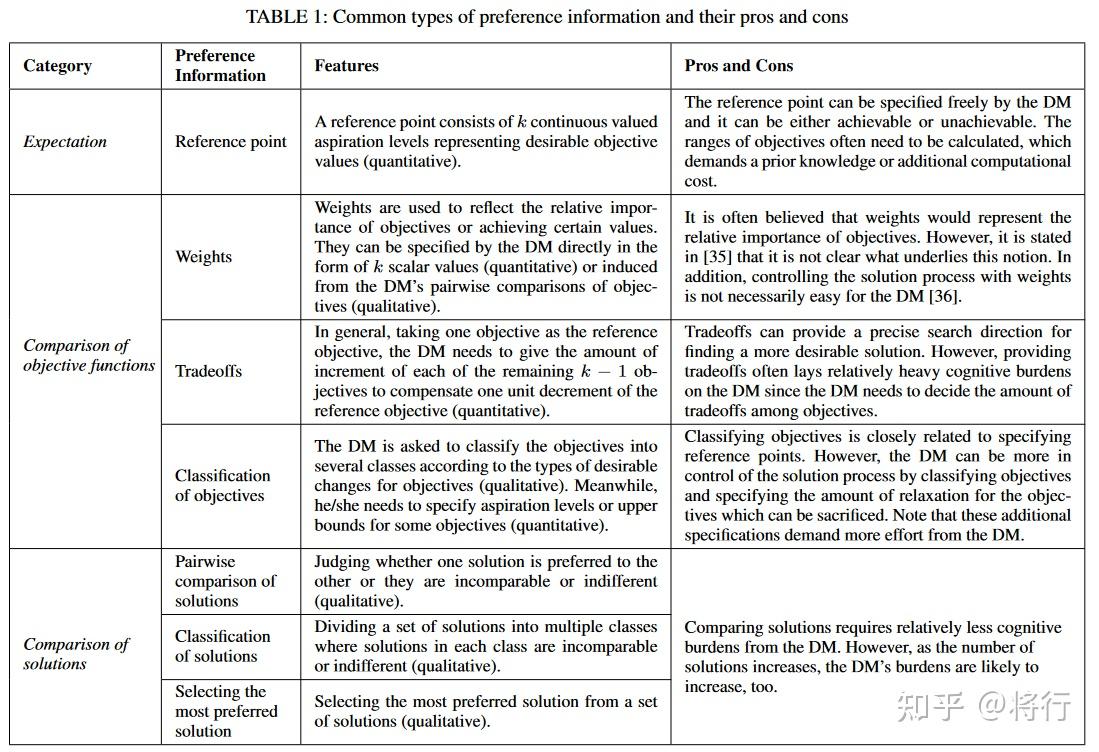
文献中常用的偏好模型有以下三种:价值函数(效用函数)、支配关系和决策规则(“value function (utility function), dominance relation, and decision rules” (Xin 等, 2018, p. 5))[41]
价值函数(VF)是所有目标的标量函数,用于定量评估解决方案。其参数由 DM 直接指定或根据 DM 的偏好间接计算。优势关系以一对解决方案的关系形式描述 DM 的偏好。在交互式 MOEAs 的选择算子中,它经常用来代替帕累托优势关系。决策规则以一组 "IF-THEN "规则来模拟 DM 的偏好。
多目标优化问题中,决策者通常根据某种隐含的价值函数来表达其偏好,价值函数可以用U=U (f1, f2, . . . , fk)来表示。通过显式的价值函数,可以对客观向量在客观空间中进行完整排名,其最优解是决策者的最佳满意解。但由于决策者不具备完整信息,他们的价值函数通常无法被明确确定。因此,很多方法会根据决策者的偏好动态地建模这一隐含的价值函数,三种流行的价值函数类型:
- 加权度量指标(“Weighted metrics” (Xin 等, 2018, p. 6))
- 加权度量衡量了客观向量与特定点之间的距离,可以是一个理想点z?或者一个拥有最大值的nadir点znad。决策者的偏好由权重反映,可以采用不同的Lp-范数,并在交互式多准则决策制定中,加权度量被制定成距离优化问题(不同的表述形式),以找到(弱)帕累托最优解。
- 成就标量函数(“Achievement scalarizing function” (Xin 等, 2018, p. 7))
- 成就标量化函数(ASF)是由Wierzbicki在参考点方法中首次引入的,既表达了实现愿望水平的效用,又表达了未能实现愿望水平的不利影响。权重可以根据决策者的偏好来逐渐保持不变或更新,例如,在[38]中提出了三种将偏好融入ASF权重的方法。交互式多准则决策方法通常使用ASFs制定最小化问题;交互式演化多目标优化方法则使用ASFs将一个种群分为多个前沿,或定义用于评估MOEA选择算子中的解的适应度函数。
- 加法效用函数(“Additive VF” (Xin 等, 2018, p. 7))
- VF的参数可以由决策者直接指定,或从决策者的偏好中学习VF;一些IMO方法不对DM的潜在VF的形式做任何先验假设,并使用神经网络和支持向量机等技术从他/她的偏好中学习VF。
支配关系表达了DM对一对解决方案的偏好:一方支配(即优先于)另一方,或者它们是不同或无法比较的。许多支配关系将Pareto支配关系与DM的偏好相结合,决策者的个人偏好可对解决方案的选择产生影响,因此无支配解决方案也可以进行比较。
Fonseca和Fleming引入了基于DM提供的渴望水平的“preferable to”关系。Sinha等人基于DM的偏好构建了一个多面体锥体。Molina等人通过使用参考点定义了g-支配关系。这些支配关系为多目标优化提供了有益的方法。
决策规则通常采用 "IF-THEN "规则的形式,更具通用性,而且由于其语法自然,DM 更容易理解。作为决策规则的一种,模糊规则可以处理 DM 的定性偏好,并将其转化为目标或解决方案的定量信息。
搜索引擎分为MP和非MP技术两类,MP技术包括线性规划、非线性规划和多目标规划等成熟的优化技术,而非MP技术则主要是启发式方法,如进化算法、禁忌搜索、模拟退火等。进化算法(EAs)强调通用性,在解决多模态、不连续、强约束和动态问题等复杂SOPs方面显示出优势,尤其是单次运行中能够找到一组(近似)帕累托最优解的能力。GA是MOEAs中最常用的EA。
应用基于 SI 的优化算法或记忆算法作为搜索引擎的优势也值得进一步研究。群体智能(SI)指一群简单的个体通过彼此之间和与环境的互动,作为一个整体展现出智能行为。典型的基于SI的优化算法包括蚁群优化、粒子群优化、人工免疫系统、蜂群优化、鱼群搜索、烟花算法、脑风暴优化等。记忆算法将进化算法(EAs)与局部搜索相结合,指导良好的局部搜索的加入可以提高MOEAs的整体性能。
IMO 方法主要分为4类:1)基于期望的方法 2)基于目标函数比较的方法 3)基于解的比较方法 4)满足不同类型偏好的方法
20世纪80年代,Wierzbicki提出了基于参考点的方法,随后在1993年,Fonseca和Fleming提出了基于参考点的交互式多目标进化算法(MOEA)。该方法使用DM的偏好来评估每一代遗传算法的种群中的解。然而,这种方法的主要缺点是DM的工作量非常大,因为他/她必须在每一代遗传算法中提供偏好。最近十年,基于参考点的MOEAs在IMO中变得普遍。Deb等人提出了R-NSGA-II,它将参考点方法与NSGA-II相结合。DM可以同时提供多个参考点,对每个参考点,计算它与当前种群中每个个体的加权欧氏距离。这样,接近所有参考点的个体将受到偏好。然而,R-NSGA-II可能会面临种群多样性下降的问题,Siad等人指出要处理多个参考点以获得令人满意的结果。此外,RD-NSGA-II和RD方法相结合,该方法投影一组点到参考方向,使用ASFs将种群分成多个前沿。但是当使用单个参考方向时,RD-NSGA-II也可能面临种群多样性降低的问题因为它不具备一种清理机制。LBS-NSGA-II 在该方法中将参考点和多属性决策分析工具结合使用,通过增强型ASF和修改outranking关系,有效减轻了决策者的负担。此外,介绍了偏好基础进化算法(PBEA)、g-优势关系、r-优势关系、切比雪夫偏好关系和加权成就标量化函数遗传算法(WASF-GA)等方法。
这些方法可同时探索多个ROI,且部分可通过参数调整获得期望的解集分布,但参数设置在解决实际问题时并不容易。
介绍了基于偏好的多目标进化算法(P-NSGA-II)和将偏好函数与多目标进化算法相结合的方法。P-NSGA-II利用高斯函数表示决策者(DM)的偏好,并通过计算偏好函数来取代NSGA-II中的拥挤距离,从而获得偏好的解集。此外,还介绍了涉及可取半径和最短距离的拓展P-NSGA-II,以及与多目标优化算法相结合的偏好函数方法。
这些方法需要DM事先指定偏好函数的参数,以表示其对目标值的期望,但也可以在优化过程中与DM进行交互,通过改变参数来调整偏好函数以获得新的期望解集。
两种基于权重的方法:一种是通过将决策者的定性偏好转化为对目标的权重,通过询问决策者对目标进行成对比较并指定重要程度,然后使用权重矩阵计算目标的权重,通过加权支配关系定义了修正的帕累托支配关系。另一种是将决策者的模糊偏好转化为权重区间,利用随机权重聚合和动态权重聚合方法将这些权重区间纳入多目标进化算法中。
此外,基于模糊逻辑的交互式多目标进化算法能够根据决策者的偏好自适应调整搜索方向和解的范围,相比于其他方法,它在找到更符合决策者偏好的解时表现更好,但时间复杂度较高。
基于梯度的交互式多目标优化方法GRIST。该方法通过使用DM提供的无差异偏好来估计潜在VF的梯度。将梯度投影到Pareto前沿的切线超平面上,提供了一种改善DM效用的新搜索方向。同时介绍了GRIST方法的独特之处,即建立必要的最优条件可促进DM的偏好引导,从而减轻DM的负担。此外,证明了其收敛性。该方法适用于线性和非线性MOPs,并且可以处理Pareto前沿在有限点处非凸或非平滑的情况。然而,由于MOPs在大多数交互式权衡方法中假设具有凸性条件,因此基于梯度投影的框架不适合用于具有断开Pareto前沿的MOPs。
Luque等人开发的PROJECT方法。该方法将GRIST方法的梯度投影框架与参考点方法相结合,实现了能够反映DM局部权衡的Pareto最优解生成。此外,提到GRIST方法将可能受限于解决MOPs的适用性问题。
Chen等人开发的T-IMO-EA方法。该方法通过与EAs相结合,可以提高GRIST方法的通用性,EAs被用作搜索引擎来生成近似Pareto最优解。通过实验证明,T-IMO-EA在使用的测试MOPs上具有比GRIST方法更好的收敛性。
基于目标分类的经典IMO方法,即非可微交互式多目标捆绑优化系统NIMBUS。在每次迭代中,允许DM将目标分类为当前解中的最多五类,以找到更理想的解决方案。使用结合加权距离度量和ASF的函数将MOP转换为约束SOP。NIMBUS适用于涉及连续或整数值变量的线性和非线性问题。已实现为WWW-NIMBUS软件系统,这是一个基于互联网的交互式优化软件。
此外,基于相同偏好信息的不同标量化函数可能导致不同的Pareto最优解的情况,因此开发了同步NIMBUS。其基本思想是使用几个基于相同偏好信息的标量化函数生成多个Pareto最优解。同步NIMBUS已实现为WWW-NIMBUS系统的4.0版本,包含四种不同的标量化函数。最终,DM可以在每次迭代中获得多个解决方案,并判断哪个是最受欢迎的。
Miettinen 等人[89]提出了 NAUTILUS 方法,旨在避免不必要的锚定效应,即 DM 将其思维固定在某些信息上,即使这些信息可能无关紧要。该方法从最低点开始,逐步同时改进所有目标。在每次迭代时,他/她还被要求对改进每个目标的相对重要性进行排序,或者指定他/她希望如何改进当前迭代解的当前目标值的百分比,当前迭代解位于上一次迭代解及其在帕累托前线上的相应投影的连接段上。DM 可以更改剩余迭代次数,也可以后退一步。NAUTILUS 方法的一个重要意义在于DM 无需在目标之间做出权衡,因为所有目标值都会得到改善。
Sindhya 等人[24]开发了一种基于偏好的交互进化算法(PIE),与 NAUTILUS 方法的理念几乎相同。主要区别在于,PIE 是一种 "EA in MCDM "方法,即使用 EA 作为搜索引擎,而不是 MP 技术来最小化每次迭代的 ASF。 EA 的每一代中,ASF 值最小的解决方案和整个群体都被存储在档案集中,以便 DM 可以轻松访问以前的解决方案。
多目标进化算法中询问决策者对解决方案进行成对比较的方法较为流行。不同的交互式多目标进化算法主要区别在于偏好模型的构建和使用偏好模型来指导搜索的方式。交互式进化元启发式算法(IEM)将决策者的解决方案成对比较转化为线性规划问题的约束,其最优解为估计的值函数的权重,用线性加权目标的形式来评估种群。但由于线性值函数的限制,这可能成为一个局限因素。渐进交互式多目标进化算法(PI-EMO-VF)要求决策者对多个解决方案进行完整排名,以确定多项式值函数,用于修改帕累托支配关系以区分解决方案。然而,该方法无法处理决策者认为有些解决方案不可比的情况,并且需要较高的计算成本。其他方法如基于支持向量机的脑-计算机进化算法(BC-EMO)和交互非支配排序算法(INSPM)也提出了各自的偏好模型估算方法,但也有各自的局限。如何在实践中确定相关参数仍然是一个问题。
上述交互式多目标进化算法均将决策者的偏好建模为VFs,以决策规则表示的偏好模型比函数或关系模型更具有一般性和可理解性。
关于解决方案分类的方法有多种,例如,DRSA-EMO和I-SIBEA等算法使用决策规则作为偏好模型。
DRSA-EMO要求决策者将一组解进行分类,分为“相对好”和“其他”。在每次迭代中,根据诱导的决策规则进行EMO程序的完整运行。解决方案根据DRSA规则匹配数的主要得分和基于拥挤距离的次要得分进行排名。在第一次交互中,向决策者呈现的解是使用蒙特卡罗方法生成的。在其他交互中,呈现的解来自EMO程序的最后人口。由于DRSA能够处理不确定性下的决策问题,因此DRSA-EMO-PCT和DRSA-EMO都可以考虑鲁棒性问题。
I-SIBEA允许决策者指定与EMO过程进行交互的次数,并根据偏好选择的解,划分可行区域并定义权重分布函数以计算后续生成中的加权超体积。解根据其对超体积的贡献被选入下一代。 I-SIBEA的一个优点是使用优选和非优选解提供更灵活的方式来引导搜索。实验证明非优选解的信息使算法更快收敛到决策者的感兴趣域。
四种基于选择最优解的交互式多目标进化算法(MOEA):包括使用多面体锥体的渐进式交互式EMO方法(PI-EMO-PC),基于凸偏好锥体的交互式MOEA,以及基于解对应权重的交互式MOEA/D算法和交互式领域定义进化算法(iTDEA)。这些方法通过引导决策者(DM)周期性地从一组解中选择最优解,来指导MOEA朝向DM的感兴趣区域(ROI)进行搜索。它们都综合考虑了DM的偏好以指导新的支配关系。这些方法允许DM选择最佳解来更新偏好的解集或者权重区域,进而聚焦搜索方向。
此外,文中还提到了一些作者对这些方法的改进建议,例如如何更好地过滤代表性解集,以及未来研究应该考虑DM一致性的影响等问题。
允许 DM 提供不同类型偏好的方法为 DM 提供了更多的选择。
iPICEA-g是一种交互式多目标进化算法,其可以根据决策者的偏好将其处理为渴望水平或目标权重。与其使用数值来指定偏好不同,决策者可以简单地在目标空间中勾画出其优选区域,而iPICEA-g可以根据这些勾画出的区域自动配置所需的参数,诸如渴望水平和权重。候选解的种群和专门生成的目标向量都是共同进化的,以引导候选解朝着偏好区域发展。iPICEA-g的主要优势在于它既能满足渴望水平或权重的偏好形式,又可同时探索多个感兴趣区域。
交互式RVEA也是基于参考向量引导的进化算法,并且能够处理决策者多种偏好类型,包括指定参考点、为每个目标提供优选范围,以及选择偏好或非偏好解。交互式RVEA可以将这些偏好转换为一个格式,即参考向量,通过使用角度惩罚距离标量化来引导种群朝着决策者的偏好区域。
IMO 中需要讨论的八个关键问题,分为三类:与 DM 相关的问题、与机器相关的问题和与整个交互系统相关的问题。
- 1) 如何减轻 DM 的负担?(Dm1)
过重的负担可能会导致 DM 在提供偏好时出错,或过早终止 IMO 方法。为了减轻决策者的负担,可以采取以下措施:
- 一是针对决策者在提供偏好时的认知负担,可以提供不同的表达方式,让决策者选择更喜欢的方式来减少负担;
- 另一是减少决策者和系统之间的互动次数,避免过多的互动导致疲劳和错误,可以在有限的互动次数内找到决策者的最佳部分(即MPS)。
- 更进一步,采用图形化的解决方案可以促进决策者对解决方案的理解和分析,并减轻其负担。
- 2) 如何处理 DM 的认知偏差?(Dm2)
认知偏见是指决策者的决策与理性决策之间的差异。正确处理决策者的认知偏见可能会减少最终解决方案与实际最佳部分(MPS)之间的差距。
其中,锚定是与交互式多目标优化(IMO)相关的一种偏见。Buchanan和Corner (115) 研究了锚定在两种IMO方法中的影响,并提出了两种锚定偏见的衡量方法。他们得出结论,起始点很重要,更具定向和结构化的解决方法更有可能支持锚定,而基于自由搜索的方法则不太可能支持。此外,由于任何起始点都可能对决策者造成偏见,因此应考虑从反映决策者初始偏好的点开始。文中描述的NAUTILUS方法通过从最低点开始,避免了锚定偏见,这样每个目标都可以得到改进,决策者可以达到任何帕累托最优解。这种方法可以在其他IMO方法中使用,以找到一个非锚定的起始点。
另一个相关的偏见是损失规避,意味着人们更倾向于避免损失,而不是获得同等额的收益。这可能阻碍决策者从一个帕累托最优解转移到另一个,因为他/她必须牺牲一个或多个目标。在NAUTILUS方法中,由于所有目标都可以同时改进,决策者总是获得益处,并且不需要在目标之间做出权衡。
- 3) 如何处理不同类型的偏好?(Dm3)
许多IMO方法要求决策者提供一种特定类型的偏好,如果决策者不擅长提供这种类型的偏好,他/她可能会犯错。因此,有必要开发能够处理不同类型偏好信息的IMO方法。
一些研究人员已经开发了综合多种IMO方法的通用交互系统,并允许决策者在每次迭代时自由选择要提供的偏好信息类型。Luque等人研究了不同类型偏好之间的关系。通过研究不同类型偏好的等价性,可以将决策者以前提供的偏好转化为当前迭代中他/她想要提供的偏好类型,从而帮助决策者提供新的偏好。
然而,Luque等人考虑的IMO方法都是多准则决策方法,并要求定量偏好。对于一些交互式多目标进化算法(MOEAs)来说,很难研究不同类型偏好之间的关系,因为偏好可能是定性的,偏好模型可能不是函数。
- 4) 如何处理不一致的偏好?(Dm4)
不一致的偏好可能导致DM提供的偏好与IMO方法的偏好模型相矛盾或不兼容。矛盾信息意味着DM对一组解决方案的排序中存在一个或多个循环,由于错误或DM偏好的演变,可能会产生矛盾信息。这可以通过删除或更改导致矛盾的偏好关系来消除,然而,Greco等人指出,不一致之处可能包含构建偏好模型的重要信息,不能简单地删除。
- 1) 如何选择/构建合适的偏好模型?(Ma1)
偏好模型的适用性和有效性值得深入调查,一个重要的关注点是不同偏好模型之间在建模不同类型偏好能力方面的关系。如果现有的偏好模型可以划分为等价类,就可以根据一些标准(如易用性,高准确性建模决策者偏好和低计算成本),从相关的等价类中选择一个或几个特定类型的偏好选择合适的偏好模型。为了适应更多类型的偏好,可以通过集成来自不同等价类的合适偏好模型构建偏好模型集合。
- 2) 如何快速找到 DM 的 MPS?(Ma2)
让决策者长时间参与解决方案的过程是不切实际的。首先,应该减少决策者每次迭代所花费的交互时间,这可以通过在可能的情况下为决策者提供清晰的信息来实现。其次,决策者可能不愿意长时间等待机器的输出,因此需要高效的搜索引擎。最后,交互次数不应太多。
对于每次迭代生成一个或多个帕累托最优解的方法,可以同时减少每次迭代的交互时间、计算时间和交互次数。然而,对于某些交互式MOEA,它们根据决策者偏好序列的指导逐步朝向决策者的投资回报率前进,减少交互次数可能会减缓种群移动速度。比如,Deb等人指出,经常提供偏好可以加速其提出的交互式MOEA的优化。在这种情况下,必须考虑计算时间和交互次数之间的权衡。
- 1) IMO 方法何时停止?(D-M1)
IMO 方法的终止是一个重要的问题。Miettinen[3]总结了三个主要的终止标准。第一个是当决策者对一个解感到满意并希望停止时。第二个是当决策者感到疲倦并不想继续时。最后一个是当满足数学终止标准时。大多学者认为 行为收敛比数学收敛更重要。
- 2) 如何评估 IMO 方法?(D-M2)
IMO的最终目标是找到决策者的最好解 (MPS),因此与人类决策者进行测试对于验证IMO方法的实用性至关重要。由于决策者可能难以给出定量值,可以让他/她用“令人满意”和“不令人满意”等自然语言表达满意度。决策者的感受很重要,因为它决定了IMO方法是否能被广泛接受和应用于实际中。
然而,人类对IMO的参与使评估IMO方法变得主观。评估结果可能会随着人类决策者的不同而变化。即使是同一位人类决策者,由于人类决策者的偶然性,结果也可能会发生变化。此外,由于人类决策者的随机性和他们对先前实验的记忆,重复此类实验是困难的。
虚拟决策者是一种有效的替代方案。常见的虚拟决策者是VF,其在搜索空间中的最优解可作为MPS。可以利用IMO方法的最优解与最终解之间的距离来评估最终解的质量。陈等人提出了一个由四种不同VF组成的虚拟决策者库,以全面而公正地比较IMO方法。与人类决策者相比,虚拟决策者更便宜、更方便,并且由于消除了人类决策者的偏见和疲劳,也更有利于重复实验。
“Reliable IMO methods are expected to adapt to different DMs and support them to find their MPSs with low human burdens and small computational cost.” (Xin 等, 2018, p. 19) 可靠的 IMO 方法有望适应不同的 DM,并支持它们以较低的人力负担和较小的计算成本找到其 MPS。
- 人类行为
DM 在 IMO 中扮演着至关重要的角色。不同 DM 的行为如何影响 IMO 方法的最终解决方案,目前还不是很清楚。有必要了解不同 DM 的行为,以便为 DM 找到其 MPS 提供适当的支持。此外,对人类行为的研究也有利于解决 Dm1 和 Dm2 问题。
- MCDM 和 EMO 方法的进一步杂交
通过将多准则决策方法(MCDM)和进化多目标优化(EMO)方法相互融合,可以实现它们的优势互补。现有的“MCDM在EMO中”的基于交互式多目标优化(IMO)方法通常要求决策者提供参考点或比较解决方案。此外,“EA在MCDM中”的基于IMO方法受到的关注较少。由于许多经典的IMO方法如STEM和NIMBUS已成功应用于解决实际多目标优化问题,因此研究将进化算法(EAs)整合到其中,以增强它们解决更多问题的能力具有一定的研究价值。
- 勘探与开发(exploration and exploitation)之间的权衡
探索和开发在搜索和优化中已被定义并讨论过,它们之间的权衡影响着计算成本和收敛质量。在交互式MOEAs中,强调探索可以为DM提供更多信息,但可能会减慢收敛速度;强调开发可能会狭窄DM对问题的视角,并导致过早的收敛。一些IMO方法使用参数来平衡探索和开发,最初,参数被设置为相对较大的值,以获得广泛的解决方案范围,然后逐渐减小以集中搜索在决策者的感兴趣区域(ROI)
- 处理语言偏好(linguistic preferences)
人类决策者更倾向于提供定性偏好而非定量偏好。鉴于这一事实,模糊逻辑是处理人类语言偏好的合适工具。它可以将模糊偏好转化为定量信息,正如文献[37]、[104]和[105]中所做的那样。因此,模糊逻辑或用于偏好提取和转化的模糊推理系统值得进一步研究。
- 交互系统
根据 Dm3 问题所述,已经开发出了一些通用交互系统,允许决策者选择他/她所需提供的偏好类型,并在每次迭代时自由更改。为了满足更多类型的偏好需求,有必要设计新的交互系统,其中包括多种不同偏好模型的IMO方法。这些偏好模型应能够建模不同类型的偏好。





